Imagine a tightrope walker, confined to a single direction – forward and backward. That’s one dimension. Now picture an ant on a tabletop, moving forward, backward, left, and right – two dimensions. Finally, envision yourself with a jetpack, soaring up and down, adding a third dimension to your movement. But what if there was a fourth, unseen dimension to explore? This beginner’s guide delves into the fascinating concept of the fourth dimension and introduces you to the mind-bending shapes that inhabit it.
The Glossary: Unlocking 4D Terminology
Understanding the fourth dimension requires a new vocabulary. Let’s explore some essential terms:
Tesseract: Consider the sequence: square, cube… what comes next? A square’s edge comprises four line segments, a cube’s surface consists of six squares, so a tesseract’s “hypersurface” comprises eight cubes. In essence, the tesseract is the four-dimensional analogue of a cube.
If $x^2$ is x squared, $x^3$ is x cubed, then perhaps $x^4$ could be called “$x$ tesseracted”?!
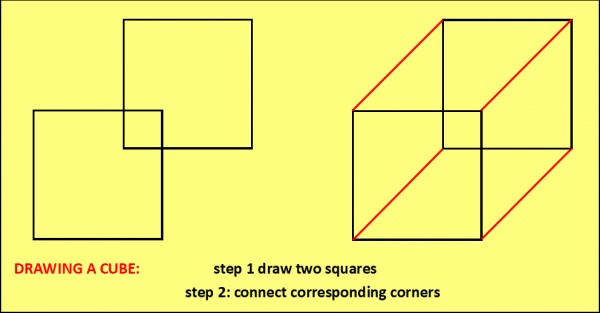
Visualizing a tesseract is challenging, but we can attempt to represent it by connecting corresponding corners of two slightly offset cubes, similar to how a cube is drawn from two offset squares.
Conceptual illustration of a tesseract depicted as a cube within a cube.
Dali Cross: This is a “net” of a tesseract, made up of 8 cubes that could “fold up” into a tesseract, much like the 6 squares of a cube net fold to make a cube. The artist Salvador Dali featured this cross in his 1954 surrealist painting “Corpus Hypercubus“. There are 11 different nets for a cube, and 261 distinct octocubal nets for a tesseract, revealing the complexity of this 4D shape.
First possible net to fold up into a standard cube.
Second possible net to fold up into a standard cube.
Hypercube: The n-dimensional analogue of a “square.” Squares, cubes, and tesseracts all fall under the umbrella of hypercubes. The term provides a general way to describe multi-dimensional cubes.
Polytope: Extending the idea of a polyhedron (“many flat sides/faces”) to four or more dimensions gives us a polytope. A polygon (e.g., triangle, octagon) is a 2D object bounded by line segments, a polyhedron (e.g., cube, pyramid) is a 3D object bounded by polygons, so a polytope (e.g., tesseract) is a 4D object bounded by polyhedra.
Cell: Consider the sequence: vertex, edge, face… what’s next? The two boundary points of an edge are vertices; the boundaries of a face are edges; the boundaries of a polyhedron are faces; and the boundaries of a 4D polytope are cells. A tesseract has 8 cube-shaped cells, mirroring how a cube has 6 square-shaped faces.
Hyperplane: In 2D space, scatter graphs have a line of best fit; in 3D space, they have a plane of best fit; in 4D space, we have a hyperplane of best fit. This represents the best fit for data points in a four-dimensional space.
Simplex: Another sequence: line segment, triangle, tetrahedron… The next step is a 4-Simplex. A triangle is a polygon bounded by three line segments; a tetrahedron is a polyhedron bounded by four triangles; a 4-Simplex is a polytope bounded by five tetrahedra. The 5D version is called a 5-Simplex.
The Importance of Exploring Higher Dimensions
Mathematics is more than just numbers; it’s the study of pattern and structure. Numbers enable us to examine these patterns, leading to abstract concepts that are best described algebraically but visually represented through geometry. Geometric visualizations offer a powerful tool for understanding algebraic concepts, so limiting our studies to the three spatial dimensions we inhabit would be a disservice to the potential of mathematical exploration. The concepts discussed in this glossary illustrate the beauty and power of mathematics beyond our everyday experiences. By visualizing higher dimensions, we gain a deeper understanding of the underlying mathematical principles that govern our universe.