What Is Guided Wavelength? It represents the distance between two points of equal phase along a waveguide, a critical parameter in microwave engineering. CONDUCT.EDU.VN offers comprehensive insights into this essential concept, providing solutions for professionals and students alike. Understanding guided wavelength is crucial for designing efficient microwave circuits, optimizing signal transmission, and minimizing signal loss.
1. Understanding Cutoff Frequencies in Waveguides
Waveguides support various modes of electromagnetic wave transmission. However, for most practical applications, the dominant mode, typically the TE10 mode in rectangular waveguides, is of primary interest. The cutoff frequency represents a critical threshold for waveguide operation.
1.1. Defining Cutoff Wavelength
The cutoff wavelength (λc) is the longest wavelength that a waveguide can support for a particular mode. For the TE10 mode in a rectangular waveguide, the cutoff wavelength is directly related to the waveguide’s width (a), specifically:
λc = 2a
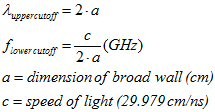Cutoff Wavelength Formula Depicting Wavelength Calculation Based on Waveguide Dimension
This equation highlights that the cutoff wavelength is twice the width of the waveguide. This relationship is fundamental in determining the operating frequency range of the waveguide.
1.2. Calculating Cutoff Frequency
The cutoff frequency (fc) is the frequency corresponding to the cutoff wavelength. It can be calculated using the following formula:
fc = c / λc
Where:
- c is the speed of light in a vacuum (approximately 3 x 10^8 meters/second).
- λc is the cutoff wavelength.
Therefore, fc = c / 2a
The cutoff frequency represents the lower limit of the operating frequency range for a specific waveguide mode. Frequencies below the cutoff frequency will be attenuated and will not propagate effectively through the waveguide.
1.3. Waveguide Operating Band
The recommended operating band for a rectangular waveguide is typically between 125% and 189% of the lower cutoff frequency. This range ensures efficient signal transmission with minimal attenuation and signal distortion. For example, for WR-90 waveguide, which has a cutoff frequency of 6.557 GHz, the recommended operating band is 8.2 to 12.4 GHz. Operating outside this range can lead to increased signal loss and reduced performance. For detailed information on waveguide loss, visit CONDUCT.EDU.VN, or our page on waveguide loss.
2. Exploring Guide Wavelength
Guide wavelength (λg) is a crucial parameter in waveguide design and analysis. It describes the effective wavelength of a signal as it propagates within the waveguide. Understanding guide wavelength is essential for designing waveguide components and systems that operate efficiently at microwave frequencies.
2.1. Defining Guide Wavelength
Guide wavelength is the distance between two equiphase planes along the waveguide. In simpler terms, it is the distance over which the phase of the electromagnetic wave changes by 2π radians within the waveguide.
2.2. Guide Wavelength Formula
The guide wavelength (λg) is related to the free-space wavelength (λ) and the cutoff wavelength (λc) by the following equation:
1/λg^2 = 1/λ^2 – 1/λc^2
Alternatively, this can be expressed as:
λg = λ / √(1 – (λ/λc)^2)
Where:
- λg is the guide wavelength.
- λ is the free-space wavelength of the signal.
- λc is the cutoff wavelength of the waveguide for the specific mode of propagation.
This formula demonstrates that the guide wavelength is always longer than the free-space wavelength. This difference arises because the waveguide confines the electromagnetic wave, causing it to propagate in a zigzag path rather than a straight line.
2.3. Factors Affecting Guide Wavelength
Several factors influence the guide wavelength in a waveguide:
- Frequency: As the frequency increases (and the free-space wavelength decreases), the guide wavelength approaches the free-space wavelength.
- Waveguide Dimensions: The cutoff wavelength, which depends on the waveguide’s dimensions, significantly affects the guide wavelength. Smaller waveguide dimensions result in a shorter cutoff wavelength and a larger guide wavelength.
- Operating Mode: Different modes of propagation within the waveguide have different cutoff wavelengths, leading to variations in the guide wavelength.
2.4. Applications of Guide Wavelength
Guide wavelength is a critical parameter in the design and analysis of various waveguide components and systems, including:
- Waveguide Filters: The guide wavelength is used to determine the physical dimensions of waveguide filters, ensuring that they operate at the desired frequencies.
- Impedance Matching Networks: Guide wavelength is essential for designing impedance matching networks in waveguides, optimizing power transfer between different components.
- Directional Couplers: The guide wavelength is used to calculate the spacing between the coupling ports in directional couplers, controlling the amount of power coupled between the ports.
- PIN Diode Switches: When designing PIN diode switches with shunt diodes spaced apart, the guide wavelength is used to determine the appropriate spacing for optimal switch performance.
3. Understanding Phase Velocity and Group Velocity
In the context of waveguides, two important concepts related to signal propagation are phase velocity and group velocity. These parameters describe how the phase and energy of the electromagnetic wave travel through the waveguide.
3.1. Defining Phase Velocity
Phase velocity (vp) is the rate at which the phase of a single-frequency wave propagates through the waveguide. It is calculated as:
vp = f * λg
Where:
- vp is the phase velocity.
- f is the frequency of the signal.
- λg is the guide wavelength.
3.2. Characteristics of Phase Velocity
- Exceeds the Speed of Light: In a waveguide, the phase velocity is always greater than the speed of light in a vacuum (c). This might seem counterintuitive, but it does not violate the laws of physics because the phase velocity does not represent the speed at which energy or information travels.
- Frequency Dependent: The phase velocity is frequency-dependent, meaning it varies with the frequency of the signal.
3.3. Defining Group Velocity
Group velocity (vg) is the speed at which the overall envelope of a wave packet, or a modulated signal, propagates through the waveguide. It represents the actual speed at which energy and information travel.
3.4. Group Velocity Formula
The group velocity can be calculated using the following formula:
vg = c^2 / vp
Alternatively, it can be expressed as:
vg = c * √(1 – (λ/λc)^2)
Where:
- vg is the group velocity.
- c is the speed of light in a vacuum.
- vp is the phase velocity.
- λ is the free-space wavelength.
- λc is the cutoff wavelength.
3.5. Characteristics of Group Velocity
- Less than the Speed of Light: The group velocity is always less than the speed of light in a vacuum (c). This is because the electromagnetic wave undergoes multiple reflections and interactions within the waveguide, slowing down its overall propagation.
- Represents Energy Propagation: The group velocity represents the speed at which the energy of the electromagnetic wave travels through the waveguide.
- Frequency Dependent: The group velocity is also frequency-dependent, varying with the frequency of the signal.
3.6. Relationship Between Phase Velocity and Group Velocity
The phase velocity and group velocity are related by the following equation:
vg * vp = c^2
This equation shows that the product of the phase velocity and the group velocity is equal to the square of the speed of light.
3.7. Practical Implications
Understanding phase velocity and group velocity is crucial for:
- Signal Integrity: Ensuring that signals propagate through the waveguide without significant distortion or delay.
- Waveguide Design: Optimizing the dimensions and characteristics of the waveguide to achieve desired performance.
- High-Speed Communication: Minimizing signal delay and maximizing data transmission rates in high-speed communication systems.
4. Delving Into Group Delay in Waveguides
Group delay is a critical parameter that characterizes the time delay experienced by different frequency components of a signal as it propagates through a waveguide. Understanding group delay is essential for designing high-performance microwave and millimeter-wave systems. For more in-depth information, explore our dedicated page on group delay here.
4.1. Defining Group Delay
Group delay (τg) is defined as the rate of change of phase shift with respect to frequency. In simpler terms, it represents the time delay experienced by the envelope of a modulated signal as it travels through the waveguide.
4.2. Group Delay Formula
The group delay can be calculated using the following formula:
τg = -dβ/dω
Where:
- τg is the group delay.
- β is the phase constant (in radians per unit length).
- ω is the angular frequency (in radians per second).
Alternatively, the group delay can be expressed as:
τg = L / vg
Where:
- L is the length of the waveguide.
- vg is the group velocity.
4.3. Factors Affecting Group Delay
Several factors influence the group delay in a waveguide:
- Frequency: Group delay is typically frequency-dependent, meaning it varies with the frequency of the signal.
- Waveguide Dimensions: The dimensions of the waveguide affect the cutoff frequency and the group velocity, which in turn influence the group delay.
- Material Properties: The dielectric constant and loss tangent of the materials used in the waveguide can also affect the group delay.
4.4. Implications of Group Delay
- Signal Distortion: Variations in group delay across the frequency band can lead to signal distortion, particularly in wideband systems.
- Pulse Broadening: In digital communication systems, group delay can cause pulse broadening, which can limit the data transmission rate.
- System Performance: Excessive group delay can degrade the overall performance of microwave and millimeter-wave systems.
4.5. Managing Group Delay
Several techniques can be used to minimize the effects of group delay:
- Waveguide Compensation: Using compensating networks to equalize the group delay across the frequency band.
- Dispersion Management: Designing waveguides with specific dispersion characteristics to minimize group delay variations.
- Operating Band Selection: Choosing an operating band where the group delay is relatively constant.
4.6. Example of Group Delay in WR-90 Waveguide
Consider a one-foot length of WR-90 waveguide. At the upper end of the operating band, the group delay approaches the free-space group delay, which is approximately one nanosecond per foot. However, near the lower cutoff frequency, the group delay increases significantly as the electromagnetic wave undergoes multiple reflections within the waveguide.
4.7. Dispersion in Waveguides
The phenomenon of electromagnetic energy traveling at different speeds over frequency is known as dispersion. Dispersion can lead to signal distortion and pulse broadening in wideband systems.
5. Practical Applications and Design Considerations
Understanding guided wavelength is crucial for designing and analyzing various microwave components and systems. Here are some practical applications and design considerations:
5.1. Waveguide Filter Design
In waveguide filter design, the guided wavelength is used to determine the physical dimensions of the filter elements, such as resonators and impedance transformers. The filter’s performance, including its center frequency, bandwidth, and insertion loss, is directly related to the guided wavelength at the operating frequency.
5.2. Impedance Matching Networks
Efficient power transfer between different waveguide components requires impedance matching. The guided wavelength is used to design impedance matching networks, such as quarter-wave transformers and stub tuners. These networks transform the impedance of one component to match that of another, minimizing reflections and maximizing power transfer.
5.3. Antenna Design
Guided wavelength plays a role in antenna design, particularly for waveguide antennas such as horn antennas and slotted waveguide antennas. The dimensions and spacing of the antenna elements are determined based on the guided wavelength to achieve the desired radiation pattern and gain.
5.4. Microwave Imaging
Microwave imaging systems use guided wavelength to determine the resolution and penetration depth of the imaging system. The guided wavelength affects how microwaves interact with the object being imaged, influencing the quality of the reconstructed image.
5.5. High-Speed Digital Circuits
In high-speed digital circuits, guided wavelength is relevant for signal integrity analysis. As signal frequencies increase, the wavelength of the signals becomes comparable to the dimensions of the circuit board traces. Understanding guided wavelength helps engineers design circuit boards that minimize signal reflections, losses, and crosstalk, ensuring reliable signal transmission.
6. Key Equations and Relationships
Here’s a summary of the key equations and relationships discussed in this article:
| Parameter | Equation | Description |
|---|---|---|
| Cutoff Wavelength | λc = 2a | Cutoff wavelength for TE10 mode in rectangular waveguide, where ‘a’ is the width of the waveguide. |
| Cutoff Frequency | fc = c / λc | Cutoff frequency, where ‘c’ is the speed of light and ‘λc’ is the cutoff wavelength. |
| Guide Wavelength | λg = λ / √(1 – (λ/λc)^2) | Guide wavelength, where ‘λ’ is the free-space wavelength and ‘λc’ is the cutoff wavelength. |
| Phase Velocity | vp = f * λg | Phase velocity, where ‘f’ is the frequency and ‘λg’ is the guide wavelength. |
| Group Velocity | vg = c^2 / vp | Group velocity, where ‘c’ is the speed of light and ‘vp’ is the phase velocity. |
| Group Delay | τg = L / vg | Group delay, where ‘L’ is the length of the waveguide and ‘vg’ is the group velocity. |
| Relationship | vg * vp = c^2 | Relationship between group velocity, phase velocity, and the speed of light. |
7. Industry Standards and Regulations
Several industry standards and regulations govern the design, testing, and operation of waveguide systems. These standards ensure interoperability, safety, and performance. Some relevant organizations and standards include:
- IEEE (Institute of Electrical and Electronics Engineers): IEEE provides standards for various aspects of microwave engineering, including waveguide components and systems.
- IEC (International Electrotechnical Commission): IEC develops international standards for electrical and electronic technologies, including waveguide-related standards.
- FCC (Federal Communications Commission): FCC regulates the use of radio frequencies in the United States, including those used in waveguide-based communication systems.
- ETSI (European Telecommunications Standards Institute): ETSI sets standards for telecommunications equipment and services in Europe, including waveguide-based systems.
8. The Importance of Accurate Measurements
Accurate measurement of guided wavelength is essential for ensuring the performance and reliability of waveguide systems. Several techniques can be used to measure guided wavelength, including:
- Slotted Line Method: This method involves using a slotted line to measure the standing wave pattern in the waveguide. The distance between two successive minima (or maxima) in the standing wave pattern corresponds to half the guided wavelength.
- Network Analyzer Method: A network analyzer can be used to measure the S-parameters of a waveguide component. The guided wavelength can be extracted from the phase response of the S-parameters.
- Time-Domain Reflectometry (TDR): TDR can be used to measure the impedance profile of a waveguide. The guided wavelength can be inferred from the time delay between reflections.
9. Overcoming Challenges in Waveguide Design
Waveguide design can present several challenges, including:
- High Frequency Operation: At high frequencies (e.g., millimeter-wave frequencies), waveguide dimensions become very small, making manufacturing and assembly more challenging.
- Losses: Waveguide losses, including conductor losses and dielectric losses, can degrade the signal quality.
- Impedance Matching: Achieving good impedance matching between different waveguide components can be difficult, especially over a wide frequency band.
- Mode Control: Ensuring that only the desired mode propagates in the waveguide can be challenging, especially in complex waveguide structures.
To overcome these challenges, engineers use advanced design techniques, such as electromagnetic simulation, optimization algorithms, and precision manufacturing processes.
10. Frequently Asked Questions (FAQ)
1. What is the difference between wavelength and guided wavelength?
Wavelength is the distance between two identical points (adjacent crests) in a propagating wave. Guided wavelength refers to the equivalent wavelength of a wave propagating in a waveguide. It is always longer than the free-space wavelength due to the waveguide’s geometry.
2. Why is the guided wavelength longer than the free-space wavelength?
The guided wavelength is longer because the waveguide structure forces the electromagnetic wave to propagate in a zig-zag path as it bounces off the waveguide walls. This elongated path increases the effective wavelength.
3. How does the cutoff frequency affect guided wavelength?
The cutoff frequency is inversely proportional to the guided wavelength. As the operating frequency approaches the cutoff frequency, the guided wavelength increases significantly, approaching infinity at the cutoff frequency.
4. What happens if the operating frequency is below the cutoff frequency?
If the operating frequency is below the cutoff frequency, the electromagnetic wave cannot propagate through the waveguide. It will be attenuated, and the signal will not be transmitted effectively.
5. What is the significance of phase velocity in a waveguide?
Phase velocity is the rate at which the phase of a single-frequency wave propagates through the waveguide. While it’s a useful parameter, it can exceed the speed of light and does not represent the actual speed of energy transfer.
6. Why is group velocity important in waveguide design?
Group velocity represents the actual speed at which energy and information travel through the waveguide. It is crucial for determining signal delay and ensuring signal integrity in high-speed communication systems.
7. How does group delay affect signal transmission in waveguides?
Group delay refers to the delay experienced by different frequency components of a signal as it travels through the waveguide. Variations in group delay can lead to signal distortion and pulse broadening, which can degrade system performance.
8. What are some common applications of waveguides?
Waveguides are used in various applications, including radar systems, satellite communication, microwave heating, and medical imaging. They are particularly useful for transmitting high-frequency signals with minimal loss.
9. What are the advantages of using waveguides compared to coaxial cables?
Waveguides typically have lower losses than coaxial cables at microwave frequencies. They can also handle higher power levels and offer better shielding against electromagnetic interference.
10. Where can I find more information about waveguide design and analysis?
CONDUCT.EDU.VN provides a wealth of information on waveguide design, analysis, and applications. You can also consult textbooks, research papers, and industry standards for more in-depth knowledge.
Navigating the complexities of guided wavelength and its applications requires expertise and reliable resources. If you’re facing challenges in understanding these concepts or need guidance in applying them to your projects, don’t hesitate to reach out to CONDUCT.EDU.VN. We provide detailed information, practical examples, and expert advice to help you succeed. Contact us at 100 Ethics Plaza, Guideline City, CA 90210, United States, or via Whatsapp at +1 (707) 555-1234. Visit our website CONDUCT.EDU.VN to explore our extensive resources and learn more. Let conduct.edu.vn be your trusted partner in mastering the intricacies of waveguide technology.
